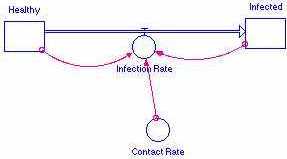
The three epidemic models can each be used to experiment with various factors to see the impact on the populations.

1. The simple epidemic model may be used to explore the impact of the contact rate variable on the healthy and infected populations. Change the contact rate and record the change in the output of the model. How does the shape of the s-shaped growth curve change? At what time does the model stabilize?
Contact Rate Stabilization Time Shape of Curve2. Exponential growth usually occurs when the rate of change is proportional to the amount present. Steady-state occurs when the system reaches equilibrium. Why does this model yield an s-shaped curve?
3. This model could be used to represent the spread of a highly contagious disease in a population living in close quarters, such as a college dorm, a military barracks, or a tribal village. This model shows how quickly a new virus could spread in a population with no immunity. What are some examples that you could use in your class?
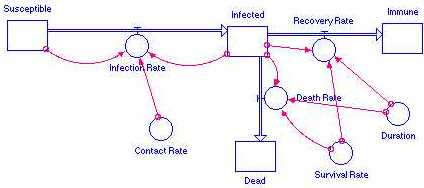
4. In a college dorm, the common cold or the flu would spread very quickly, but infected students would recover. This model could be used to experiment with disease duration and survival rate to see the effect on the population. By altering contact rate, duration or survival rate, try to achieve the following goals:
a) There are no susceptible people left
b) All people become immune
c) The entire population dies
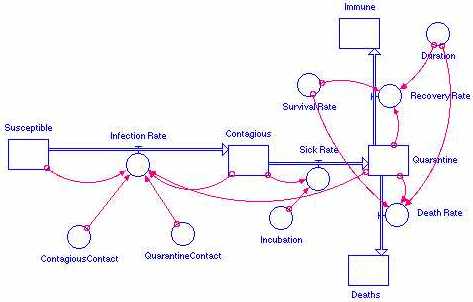
5. Childhood diseases like chicken pox fit this model, as do more serious illnesses such as Ebola or aids. We can use this model to see the effect that Incubation Time and Quarantine Contact have on the population. Adapt the model to fit each of these diseases:
a) chicken pox - high recovery rate, 1 week duration, 2 week incubation
b) Ebola - airborne virus that is highly contagious, 1 week incubation, low recovery rate, 3 week duration
c) Aids - low recovery rate, 1 year duration, 5 years incubation, highly contagious in certain conditions