Building a Savings Financial Model in Stella

SC '96

Prepared by John Biggerstaff

The problem:

The goal of this problem is to learn to build a simple financial model comparing different approaches to saving for retirement. This is a classical problem of when it is best to save. I like for you to build a model which would allow you to compare the life savings of two savers who have different approaches.

Sally will save $2,000 each year for the first 10 years that she works. She will then relax and let her investments accumulate through interest for the next 30 years for her retirement. She assumes that it is best to invest early.

Bob figures that he will earn more later and thus it will be better to save then. He saves nothing the first 10 years. He then saves $2,000 for each of the next 30 years and lets interest go to work for him on those investments.

Model #1:

Assumptions:

All of the above.

Interest is a flat rate for the entire 40 years (7% for a beginning value).

Pieces needed:

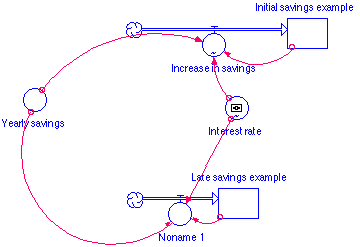
A stock for savings to accumulate in for each saver.

A flow for each stock that pumps savings into the stocks.

A converter in which we will store the interest rate.

A converter in which we will store the yearly investment.

Appropriate connectors.

Formulas needed:

An equation which determines how much new money will be pumped into each savers stock each year.

A logical (if..then) statement to determine when to apply the yearly investment.

Top level graphical interface:

We want a graph that will help us to determine which saver comes out ahead at the end of the forty years.

We want a table that will indicate the exact amounts each saver will have for each year.

We would like to have an interactive slide bar at the top level to allow us to modify the interest rate.

Use your model to examine:

Who has more at the end of the 40 years if the interest rate is 7%? 5% 6% 8%

At what interest rate will they end up with the same savings?

Do you suppose that the yearly investment makes any difference?

Financial Model 2:

This should be the same problem as number 1 with the exception that we would like to use the actual interest rates for the past 40 years. I have included in the space below the average fed-funds rate for each of the past 40 years. It isn't perfect as per the interest rates but it is at least proportional to what the savers would have achieved.

Changes needed:

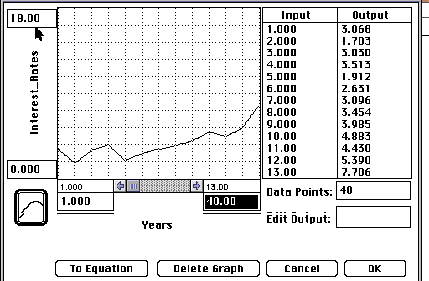
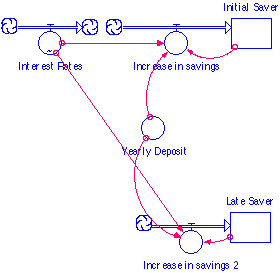
You will need to build a flow for the interest rate instead of a converter. When you set its formula you will need to use the variable "TIME". Once you have entered that variable, click on the "become a graph" button. It will then be necessary for you to enter the 40 values in the output column and to insure that the TIME column follows the appropriate beginning and ending values.

Examine:

What is the effect of this input of varying interest rates?

Try changing the graph of interest rates by predicting the future and see what modifications in rates change the winner.

1	3.068	1957	21	5.248	1977
2	1.703	1958	22	7.371	1978
3	3.03	1959	23	10.597	1979
4	3.513	1960	24	12.707	1980
5	1.912	1961	25	17.134	1981
6	2.631	1962	26	12.886	1982
7	3.096	1963	27	9.032	1983
8	3.454	1964	28	10.308	1984
9	3.985	1965	29	8.225	1985
10	4.883	1966	30	7.086	1986
11	4.43	1967	31	6.615	1987
12	5.39	1968	32	7.264	1988
13	7.706	1969	33	9.226	1989
14	7.791	1970	34	8.256	1990
15	4.782	1971	35	6.178	1991
16	4.319	1972	36	3.791	1992
17	7.928	1973	37	3.025	1993
18	10.699	1974	38	3.805	1994
19	6.454	1975	39	5.782	1995
20	5.113	1976	40	5.365	1996

Model #1

Model #2

Table